Wyjaśnienie pętli for

Pętla for to konstrukcja programistyczna, która pozwala na wykonywanie określonego bloku kodu wielokrotnie, zazwyczaj w oparciu o znaną liczbę iteracji. Jej działanie opiera się na trzech głównych komponentach:

1. Inicjalizacja: W tym kroku ustalana jest początkowa wartość licznika, który będzie kontrolował liczbę iteracji. Może to być np. liczba całkowita rozpoczynająca się od zera.

2. Warunek: Pętla sprawdza, czy dany warunek jest spełniony przed każdą iteracją. Jeśli warunek jest prawdziwy, blok kodu zostaje wykonany. Gdy warunek przestaje być prawdziwy, pętla kończy swoje działanie.

3. Inkrementacja (lub dekrementacja): Po wykonaniu bloku kodu, licznik jest modyfikowany w określony sposób (np. zwiększany lub zmniejszany). To pozwala na kontrolowanie liczby powtórzeń.

Pętla for jest szczególnie przydatna, gdy liczba iteracji jest znana z góry, co czyni ją efektywnym narzędziem do przetwarzania danych w kolekcjach, tablicach czy do wykonywania operacji w ustalonym zakresie.

Podobnie jak w przypadku pętli while, tutaj również możemy przyrównać to do drogi z rondem. Poniżej znajduje się ilustracja dla przypomnienia.

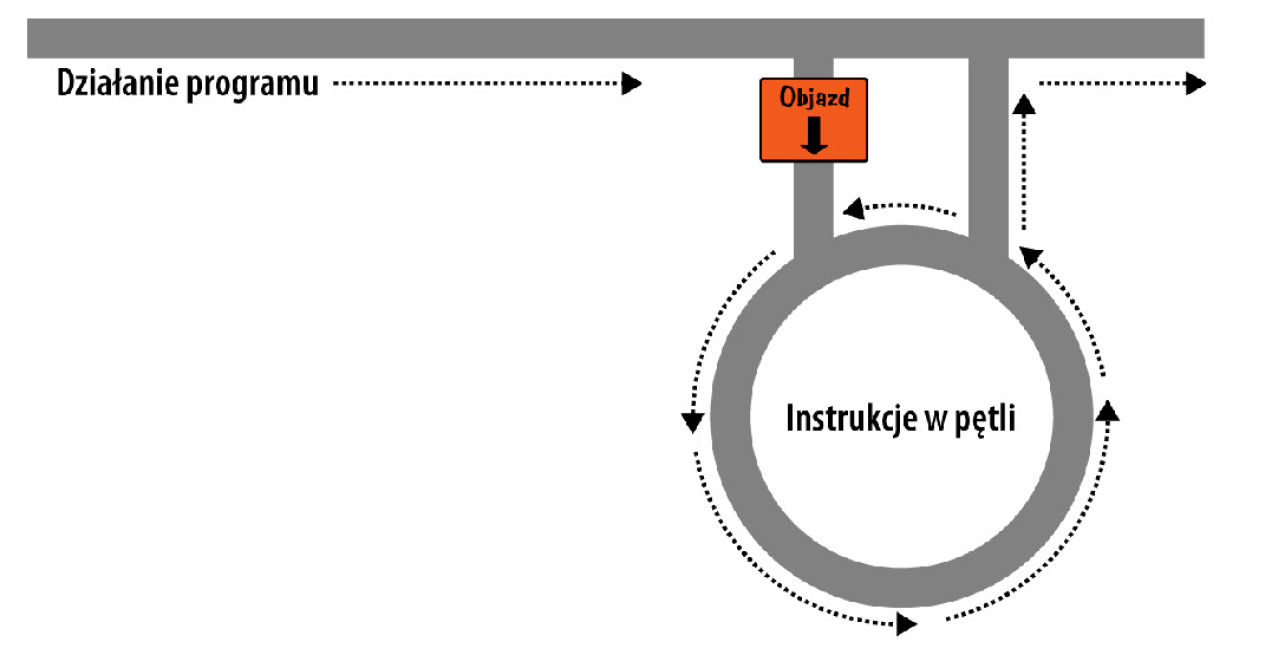
Źródło: slideshare.net

Schemat blokowy działania pętli for opisuje sekwencję operacji, które są wykonywane wielokrotnie, aż do spełnienia określonych warunków. Oto jak wygląda typowy schemat blokowy pętli for:

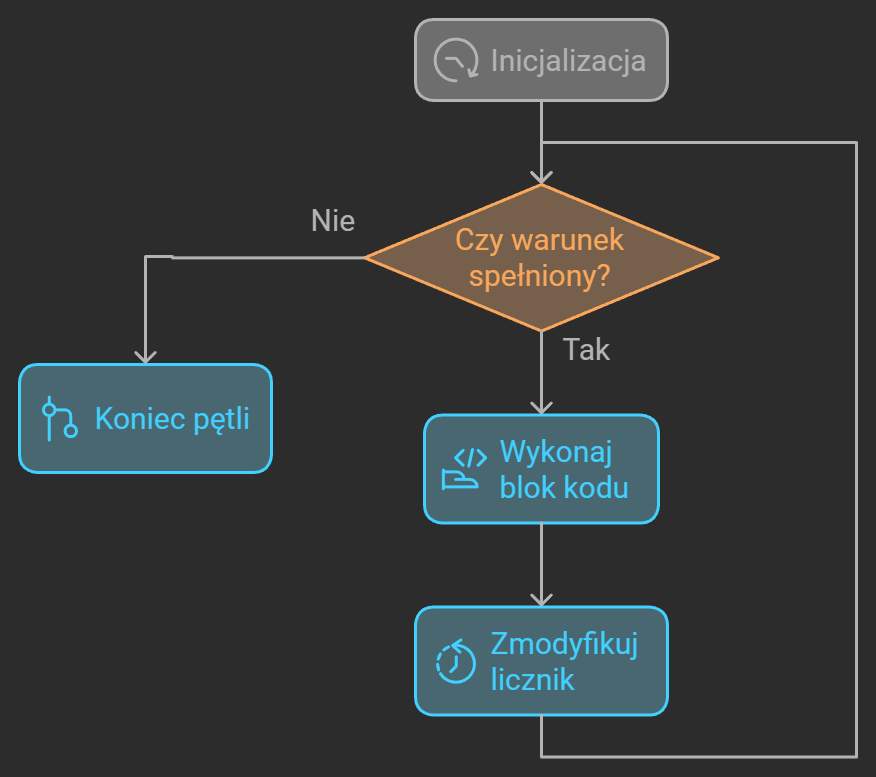
Źródło: Jakub Piskorowski

Zastosowanie pętli for w C++

Pętla for w C++ ma następującą składnię:

for (inicjalizacja; warunek; inkrementacja) {
    // Blok instrukcji do wykonania
}

Wyjaśnienie:

• for: Słowo kluczowe for rozpoczyna definicję pętli.

• inicjalizacja: To miejsce, w którym inicjalizowane są zmienne sterujące pętlą. Zwykle jest to przypisanie wartości początkowej.

• warunek: Warunek w nawiasach () jest sprawdzany przed każdą iteracją. Dopóki warunek jest prawdziwy (true), blok instrukcji będzie wykonywany.

• inkrementacja: To część, która określa, w jaki sposób zmieniają się zmienne sterujące po każdej iteracji (np. zwiększenie wartości o 1).

• Blok instrukcji: Instrukcje zawarte w bloku między { } są wykonywane, gdy warunek jest spełniony.

Przykład 1

W poniższym przykładzie zmienna i zaczyna z wartością 0, a pętla działa tak długo, jak i jest mniejsze od 5.

for(int i = 0; i < 5; i++)
{
    // Wypisz liczby
    cout << "i wynosi: " << i << endl;
}

Działanie:

• Początkowy stan: Zmienna i ma wartość 0.

• Warunek: Sprawdzany jest warunek i < 5. Dopóki jest on prawdziwy, pętla będzie się wykonywać.

• Treść pętli:

  • Każdorazowo wypisuje na ekranie komunikat i wynosi: .

  • Zmienna i zwiększa się o 1 po każdej iteracji.

• Koniec pętli: Gdy i osiągnie wartość 5, warunek i < 5 przestanie być prawdziwy, więc pętla zakończy swoje działanie.

Pętla wykonuje sprawdzenie warunku przed każdą iteracją, co oznacza, że jeśli początkowy warunek byłby fałszywy, pętla nie wykonałaby się ani razu.

Wynik działania programu:

i wynosi: 0
i wynosi: 1
i wynosi: 2
i wynosi: 3
i wynosi: 4

Przykład 2

W poniższym przykładzie pętla wypisuje wszystkie liczby parzyste od 0 do 8.

for(int i = 0; i <= 8; i += 2)
{
    // Wypisz liczby parzyste
    cout << "Liczba parzysta: " << i << endl;
}

Działanie:

• Początkowy stan: Zmienna i ma wartość 0.

• Warunek: Sprawdzany jest warunek i <= 8. Dopóki jest on prawdziwy, pętla będzie się wykonywać.

• Treść pętli:

  • Każdorazowo wypisuje na ekranie komunikat Liczba parzysta: .

  • Zmienna i zwiększa się o 2 po każdej iteracji.

• Koniec pętli: Gdy i osiągnie wartość większą niż 8, warunek i <= 8 przestanie być prawdziwy, więc pętla zakończy swoje działanie.

Pętla wykonuje sprawdzenie warunku przed każdą iteracją, co oznacza, że jeśli początkowy warunek byłby fałszywy, pętla nie wykonałaby się ani razu.

Wynik działania programu:

Liczba parzysta: 0
Liczba parzysta: 2
Liczba parzysta: 4
Liczba parzysta: 6
Liczba parzysta: 8

Przykład 3

W poniższym przykładzie pętla wypisuje kolejne liczby w odwrotnej kolejności, zaczynając od 5 do 1.

for(int i = 5; i > 0; i--)
{
    // Wypisz liczby w odwrotnej kolejności
    cout << "i wynosi: " << i << endl;
}

Działanie:

• Początkowy stan: Zmienna i ma wartość 5.

• Warunek: Sprawdzany jest warunek i > 0. Dopóki jest on prawdziwy, pętla będzie się wykonywać.

• Treść pętli:

  • Każdorazowo wypisuje na ekranie komunikat i wynosi: .

  • Zmienna i zmniejsza się o 1 po każdej iteracji.

• Koniec pętli: Gdy i osiągnie wartość 0, warunek i > 0 przestanie być prawdziwy, więc pętla zakończy swoje działanie.

Pętla wykonuje sprawdzenie warunku przed każdą iteracją, co oznacza, że jeśli początkowy warunek byłby fałszywy, pętla nie wykonałaby się ani razu.

Wynik działania programu:

i wynosi: 5
i wynosi: 4
i wynosi: 3
i wynosi: 2
i wynosi: 1

Zagnieżdżona pętla for w C++

Zagnieżdżona pętla for to pętla, która znajduje się wewnątrz innej pętli for. Tego rodzaju konstrukcja pozwala na wielokrotne iteracje, przy czym każda iteracja zewnętrznej pętli powoduje, że wewnętrzna pętla wykonuje pełny cykl swoich iteracji. Takie rozwiązanie jest użyteczne np. w przypadku pracy z macierzami lub generowania złożonych wzorców.

Struktura i działanie zagnieżdżonej pętli for:

for (int i = 0; i < 3; i++) {
    for (int j = 0; j < 3; j++) {
        // Ciało wewnętrznej pętli
        cout << "i = " << i << ", j = " << j << endl;
    }
}

Działanie:

1. Zewnętrzna pętla (i):

   • Rozpoczyna od wartości 0 i działa, dopóki spełniony jest warunek i < 3. Zmienna i jest zwiększana o 1 po każdej iteracji.

2. Wewnętrzna pętla (j):

   • Za każdym razem, gdy wykonuje się jedna iteracja zewnętrznej pętli, wewnętrzna pętla zaczyna pełny cykl swoich iteracji.

   • Zmienna j zaczyna od 0, działa do momentu, aż j < 3, i zwiększa się o 1 po każdej iteracji.

3. Działanie wewnętrzne:

   • W każdej iteracji wewnętrznej pętli wypisywane są wartości i i j.

   • Zewnętrzna pętla nie zakończy swojej iteracji, dopóki wewnętrzna pętla nie zakończy swojego cyklu (wszystkich iteracji dla danego i).

4. Przykład wykonania:

   • Gdy i = 0, wewnętrzna pętla działa z j od 0 do 2.

   • Gdy i = 1, wewnętrzna pętla działa z j od 0 do 2.

   • Gdy i = 2, wewnętrzna pętla działa z j od 0 do 2.

Wynik działania powyższego kodu:

i = 0, j = 0
i = 0, j = 1
i = 0, j = 2
i = 1, j = 0
i = 1, j = 1
i = 1, j = 2
i = 2, j = 0
i = 2, j = 1
i = 2, j = 2

Zastosowania:

• Praca z macierzami: Zagnieżdżone pętle często stosuje się do przetwarzania danych w strukturach dwuwymiarowych, takich jak tablice czy macierze.

• Generowanie wzorców: Używane do tworzenia wzorców liczbowych, znakowych, lub geometrycznych na ekranie.

Schemat działania:

1. Zewnętrzna pętla inicjuje zmienną i.

2. Dla każdej wartości i, wewnętrzna pętla wykonuje pełny cykl swoich iteracji.

3. Po zakończeniu wewnętrznej pętli, zewnętrzna pętla inkrementuje i i uruchamia ponownie wewnętrzną pętlę dla nowej wartości i.

4. Proces trwa aż zewnętrzna pętla zakończy swoje iteracje.

Zagnieżdżone pętle for są więc mechanizmem iteracyjnym, pozwalającym na wykonywanie wielokrotnych operacji w sposób skoordynowany.

Schemat blokowy przedstawiający działanie zagnieżdżonej pętli for:

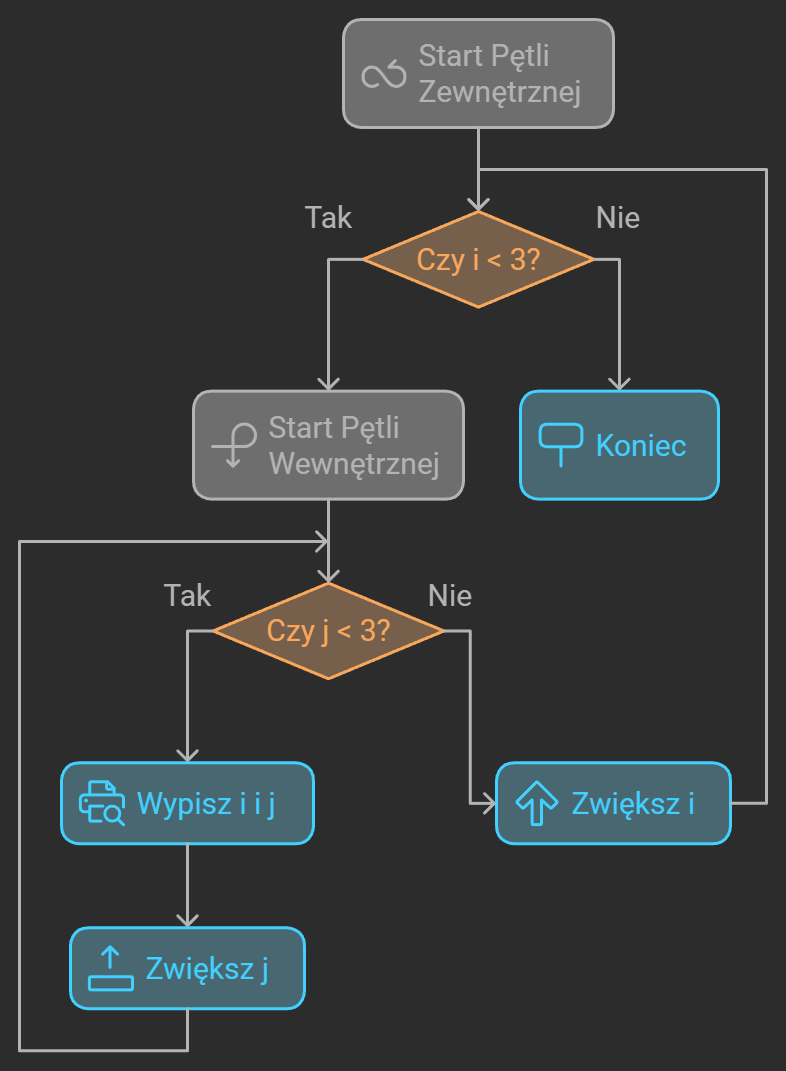
Źródło: Jakub Piskorowski

Przykład 1 - Tworzenie prostokąta za pomocą znaków *

W poniższym przykładzie zagnieżdżona pętla for jest używana do generowania prostokąta o wymiarach wysokość x szerokość, gdzie wymiary zostaną podane przez użytkownika.

int wysokosc, szerokosc;

// Poproś użytkownika o podanie wymiarów prostokąta
cout << "Podaj wysokosc prostokata: ";
cin >> wysokosc;
cout << "Podaj szerokosc prostokata: ";
cin >> szerokosc;

// Zewnętrzna pętla iteruje przez wiersze
for (int i = 0; i < wysokosc; i++) {
    // Wewnętrzna pętla iteruje przez kolumny
    for (int j = 0; j < szerokosc; j++) {
        // Wypisz znak *
        cout << "* ";
    }
    // Przejdź do nowej linii po każdym wierszu
    cout << endl;
}

Działanie:

• Początkowy stan: Program prosi użytkownika o podanie wymiarów prostokąta (wysokość i szerokość).

• Zewnętrzna pętla:

  • Pętla zewnętrzna iteruje przez i, co odpowiada liczbie wierszy prostokąta (od 0 do wysokość - 1).

• Wewnętrzna pętla:

  • Pętla wewnętrzna iteruje przez j, co odpowiada liczbie kolumn prostokąta (od 0 do szerokość - 1).

  • W każdej iteracji wewnętrznej pętli program wypisuje znak *, co tworzy jedną kolumnę prostokąta.

• Nowa linia:

  • Po zakończeniu wewnętrznej pętli, program przechodzi do nowej linii, co umożliwia wypisanie następnego wiersza prostokąta.

Podsumowanie:

Zagnieżdżona pętla for w tym przykładzie umożliwia wygenerowanie prostokąta z użyciem znaków *, gdzie zewnętrzna pętla odpowiada za tworzenie wierszy, a wewnętrzna za kolumny.

Wynik działania programu:

Podaj wysokosc prostokata: 3
Podaj szerokosc prostokata: 5

* * * * * 
* * * * * 
* * * * * 

Przykład 2 - Tablica mnożenia

W poniższym przykładzie zagnieżdżona pętla for jest używana do generowania i wyświetlania tablicy mnożenia dla liczb od 1 do N, gdzie N zostanie podane przez użytkownika.

int N;

// Popros uzytkownika o podanie liczby N
cout << "Podaj liczbe N: ";
cin >> N;

// Zewnetrzna petla iteruje przez liczby od 1 do N
for (int i = 1; i <= N; i++) {
    // Wewnetrzna petla iteruje przez liczby od 1 do N
    for (int j = 1; j <= N; j++) {
        // Wypisz iloczyn i*j
        cout << i * j << "\t"; // \t to znak tabulacji, aby wyrownac kolumny
    }
    // Przejdz do nowej linii po kazdym wierszu
    cout << endl;
}

Działanie:

• Początkowy stan: Program prosi użytkownika o podanie liczby N, dla której zostanie wygenerowana tablica mnożenia.

• Zewnętrzna pętla:

  • Pętla zewnętrzna iteruje przez i, co odpowiada liczbie, przez którą będziemy mnożyć (od 1 do N).

• Wewnętrzna pętla:

  • Pętla wewnętrzna iteruje przez j, co odpowiada liczbie, którą będziemy mnożyć przez i (od 1 do N).

  • W każdej iteracji wewnętrznej pętli program wypisuje iloczyn i * j, a użycie znaku tabulacji (\t) sprawia, że kolumny są lepiej wyrównane.

• Nowa linia:

  • Po zakończeniu wewnętrznej pętli program przechodzi do nowej linii, aby rozpocząć nowy wiersz tablicy mnożenia.

Podsumowanie:

Zagnieżdżona pętla for w tym przykładzie umożliwia wygenerowanie tablicy mnożenia, gdzie zewnętrzna pętla reprezentuje mnożoną liczbę, a wewnętrzna liczbę mnożną.

Wynik działania programu:

Podaj liczbe N: 3

1	2	3	
2	4	6	
3	6	9	

Przykład 3 - Macierz z numerami pozycji (wiersz, kolumna)

W poniższym przykładzie zagnieżdżona pętla for jest używana do wypisania macierzy, w której każda pozycja zawiera numer wiersza i kolumny. Użytkownik podaje liczbę wierszy i kolumn, a program wypisuje macierz o takich wymiarach.

int wiersze, kolumny;

// Popros uzytkownika o podanie liczby wierszy i kolumn
cout << "Podaj liczbe wierszy: ";
cin >> wiersze;
cout << "Podaj liczbe kolumn: ";
cin >> kolumny;

// Zewnetrzna petla iteruje przez wiersze macierzy
for (int i = 1; i <= wiersze; i++) {
    // Wewnetrzna petla iteruje przez kolumny macierzy
    for (int j = 1; j <= kolumny; j++) {
        // Wypisz numer wiersza i kolumny w formacie (wiersz, kolumna)
        cout << "(" << i << "," << j << ") ";
    }
    // Przejdz do nowej linii po kazdym wierszu
    cout << endl;
}

Działanie:

• Początkowy stan: Program prosi użytkownika o podanie liczby wierszy i kolumn.

• Zewnętrzna pętla:

  • Pętla zewnętrzna iteruje przez wiersze macierzy (od 1 do liczby wierszy).

• Wewnętrzna pętla:

  • Pętla wewnętrzna iteruje przez kolumny macierzy (od 1 do liczby kolumn).

  • W każdej iteracji wypisuje numer pozycji w formacie (wiersz, kolumna).

• Nowa linia:

  • Po zakończeniu iteracji wewnętrznej pętli program przechodzi do nowej linii, aby oddzielić wiersze macierzy.

Podsumowanie:

Zagnieżdżona pętla for w tym przykładzie wypisuje macierz z dokładnymi pozycjami w formacie (wiersz, kolumna), gdzie wiersze i kolumny są podawane przez użytkownika.

Wynik działania programu:

Podaj liczbe wierszy: 3
Podaj liczbe kolumn: 4

(1,1) (1,2) (1,3) (1,4) 
(2,1) (2,2) (2,3) (2,4) 
(3,1) (3,2) (3,3) (3,4) 

Zadania - pętla for w C++

Zadanie 1 - Sumowanie liczb od 1 do N

Napisz program, który obliczy sumę wszystkich liczb od 1 do N, gdzie N zostanie podane przez użytkownika. Użyj pętli for, aby wykonać to zadanie.

• Poproś użytkownika o podanie liczby całkowitej dodatniej N.

• Użyj pętli for, aby dodać wszystkie liczby od 1 do N i wyświetlić wynik sumy na ekranie.

• Po wyświetleniu wyniku zakończ działanie programu.

Wynik działania programu:

Podaj liczbę N: 5

Suma liczb od 1 do 5 wynosi: 15

Zadanie 2 - Wyświetlanie kwadratów liczb

Napisz program, który obliczy i wyświetli kwadraty kolejnych liczb od 1 do N, gdzie N zostanie podane przez użytkownika. Użyj pętli for, aby wykonać to zadanie.

• Poproś użytkownika o podanie liczby całkowitej N.

• Użyj pętli for, aby obliczyć i wyświetlić kwadrat każdej liczby od 1 do N.

• Po wyświetleniu kwadratów zakończ działanie programu.

Wynik działania programu:

Podaj liczbę N: 5

Kwadraty liczb od 1 do 5:
1^2 = 1
2^2 = 4
3^2 = 9
4^2 = 16
5^2 = 25

Zadanie 3 - Liczby nieparzyste od 1 do N

Napisz program, który wyświetli wszystkie liczby nieparzyste od 1 do N, gdzie N zostanie podane przez użytkownika. Użyj pętli for, aby wykonać to zadanie.

• Poproś użytkownika o podanie liczby całkowitej N.

• Użyj pętli for, aby sprawdzić i wyświetlić wszystkie liczby nieparzyste od 1 do N na ekranie.

• Po wyświetleniu wszystkich liczb nieparzystych zakończ działanie programu.

Wskazówka:

Aby rozwiązać to zadanie, możesz użyć pętli for, która będzie iterować od 1 do N. W każdej iteracji sprawdzisz, czy liczba jest nieparzysta. Jeśli jest nieparzysta, wypiszesz ją na ekranie.

Wynik działania programu:

Podaj liczbę N: 10

Liczby nieparzyste od 1 do 10:
1
3
5
7
9

Zadanie 4 - Liczby nieparzyste w macierzy

Napisz program, który poprosi użytkownika o podanie liczby wierszy i kolumn, a następnie wypełni macierz o podanych wymiarach liczbami nieparzystymi w kolejności rosnącej, zaczynając od 1. Każda liczba nieparzysta powinna być umieszczona w kolejnej pozycji macierzy, a po zakończeniu wypełniania program powinien wypisać zawartość macierzy w odpowiednim formacie.

Kroki do wykonania:

1. Poproś użytkownika o podanie liczby wierszy i kolumn.

2. Użyj zagnieżdżonej pętli for, aby przejść przez wiersze i kolumny.

3. Wypełniaj macierz kolejnymi liczbami nieparzystymi, zaczynając od 1.

4. Wypisz zawartość macierzy w odpowiednim formacie po zakończeniu iteracji.

Wynik działania programu:

Podaj liczbe wierszy: 3
Podaj liczbe kolumn: 4

1    3    5    7    
9   11   13   15    
17  19   21   23  

Zadanie 5 - Tabliczka mnożenia w formacie iloczynów

Napisz program, który wyświetli tabliczkę mnożenia od 1 do N w formacie a * b = wynik, gdzie N zostanie podane przez użytkownika. Program powinien użyć zagnieżdżonej pętli for, aby dla każdej pary liczb z zakresu od 1 do N wyświetlić iloczyn.

Kroki do wykonania:

1. Poproś użytkownika o podanie liczby N.

2. Użyj zagnieżdżonej pętli for do iteracji przez wszystkie liczby od 1 do N.

3. Wypisz wynik mnożenia w formacie a * b = wynik dla każdej kombinacji liczb.

Wynik działania programu:

Podaj liczbe N: 3

1 * 1 = 1
1 * 2 = 2
1 * 3 = 3

2 * 1 = 2
2 * 2 = 4
2 * 3 = 6

3 * 1 = 3
3 * 2 = 6
3 * 3 = 9

Zadanie 6 - Rysowanie ramki prostokąta z gwiazdek

Napisz program, który poprosi użytkownika o podanie szerokości i wysokości prostokąta, a następnie wyświetli ramkę prostokąta utworzoną z gwiazdek *. Program powinien użyć zagnieżdżonej pętli for, aby narysować ramkę, gdzie:

• Pierwszy i ostatni wiersz będą całkowicie wypełnione gwiazdkami.

• Pierwsza i ostatnia kolumna będą całkowicie wypełnione gwiazdkami.

• W pozostałych przypadkach, czyli środek, będzie pusty (spacje).

Wynik działania programu:

Podaj szerokosc: 10
Podaj wysokosc: 5

**********
*        *
*        *
*        *
**********

Zadanie 7 - Rysowanie dywanu

Napisz program, który poprosi użytkownika o podanie szerokości i wysokości dywanu, a następnie wyświetli wzór dywanu, który:

• Ma górną i dolną krawędź złożoną z myślników -.

• Ma boczne krawędzie (pierwsza i ostatnia kolumna) złożone z pionowych kresek |.

• Wnętrze dywanu składa się z naprzemiennych znaków # i *, tworzących szachownicę.

Program powinien użyć zagnieżdżonej pętli for, aby narysować dywan zgodnie z podanymi zasadami.

Kroki do wykonania:

1. Poproś użytkownika o podanie szerokości i wysokości.

2. Użyj zagnieżdżonej pętli for, aby iterować przez wiersze i kolumny dywanu:

   • Pierwszy i ostatni wiersz powinny być wypełnione myślnikami -.

   • Pierwsza i ostatnia kolumna wewnętrznych wierszy powinny być pionowymi kreskami |.

   • Wnętrze wierszy tworzy naprzemienne znaki # i * na podstawie sumy indeksów wiersza i kolumny.

Wynik działania programu:

Podaj szerokosc: 10
Podaj wysokosc: 5

----------
|#*#*#*#*|
|*#*#*#*#|
|#*#*#*#*|
----------

Zadanie 8 - Odwrócony trójkąt

Napisz program, który poprosi użytkownika o podanie szerokości oraz wysokości, a następnie wyświetli odwrócony trójkąt z gwiazdek *. Program powinien narysować trójkąt, gdzie szerokość podstawy odpowiada podanej szerokości, a liczba wierszy odpowiada podanej wysokości. Gwiazdki są rozmieszczone w taki sposób, że w każdym kolejnym wierszu margines po bokach trójkąta zwiększa się o jeden znak spacji, aż do osiągnięcia wierzchołka.

Kroki do wykonania:

1. Poproś użytkownika o podanie szerokości i wysokości.

2. Zainicjuj zmienną margin, która będzie określać liczbę spacji na początku i końcu wiersza.

3. Użyj zagnieżdżonej pętli for do iteracji przez wiersze i kolumny:

   • W każdej iteracji wiersza zwiększaj margin o 1.

   • Wypisz gwiazdki w zakresie od 'margin' do 'szerokosc-margin-1', a resztę wypełnij spacjami.

Wynik działania programu:

Podaj szerokosc: 10
Podaj wysokosc: 5

**********
 ******** 
  ******  
   ****   
    **    

Zadanie 9 - Liczby bez powtórzeń

Napisz program, który wyświetli wszystkie liczby trzycyfrowe złożone z różnych cyfr. Program powinien znaleźć wszystkie możliwe kombinacje liczb trzycyfrowych, gdzie każda cyfra jest inna, tzn. żadna cyfra nie powtarza się w danej liczbie. Program powinien także policzyć, ile takich liczb udało się wygenerować.

Kroki do wykonania

1. Użyj zagnieżdżonej pętli for, aby przejść przez wszystkie możliwe kombinacje cyfr od 0 do 9.

2. Sprawdź, czy wszystkie cyfry w liczbie są różne.

3. Jeśli cyfry są różne, wypisz daną liczbę.

4. Na końcu wypisz liczbę wszystkich możliwych kombinacji.

Wynik działania programu:

102
103
104
105
106
107
108
109
120
123
...
987
Liczb bez powtarzajacych sie cyfr: 648