Wyszukiwanie binarne - teoria

Algorytm szuka danego elementu w tablicy uporządkowanej (posortowanej). Jest realizowany metodą "dziel i zwyciężaj". Dzieli on tablicę na mniejsze podtablice do momentu wyszukania pozycji elementu szukanego.

Przykład

Przeanalizujmy następujący zbiór 8 uporządkowanych liczb:
1, 2, 5, 8, 9, 11, 15, 20 Potrzebne będą nam trzy zmienne pomocnicze:

• l − przechowuje numer lewego krańca tablicy,

• p − przechowuje numer prawego krańca tablicy,

• sr − przechowuje numer środkowego elementu tablicy.

W pierwszym kroku algorytmu ustawiamy:

int l = 0;
int p = 7;
int sr = (l+p)/2;

Źródło: Jakub Piskorowski

Następnie sprawdzamy czy szukany element znajduje się na pozycji sr. Jeśli tak to znaleźliśmy daną liczbę, w przeciwnym przypadku sprawdzamy czy szukana liczba jest mniejsza czy większa niż liczba znajdująca się na środkowej pozycji.

Jeśli jest mniejsza, tzn., że mamy do przeszukania lewą część badanej tablicy. Zmieniamy wartość zmiennej.

p = sr−1

a więc:

Źródło: Jakub Piskorowski

W przypadku gdy jest większa to przeszukujemy prawą część tablicy. Zmieniamy wartość zmiennej l na:

l = sr + 1

a więc:

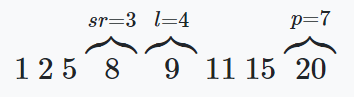
Źródło: Jakub Piskorowski

Czynność tą powtarzamy do momentu znalezienia szukanej wartości, lub gdy zmienne l i r spełnią warunek: l > r. W takim przypadku element nie występuje w zbiorze liczb.

Pseudokod - wyszukiwanie binarne

Funkcja algorytmu

Wejście funkcji:

• szukana- poszukiwana liczba

• tab[15]- tablica z posortowanymi wartościami (2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47)

Wyjście funkcji:

• pozycja- indeks (pozycja) tablicy na której znajduje się poszukiwana wartość

Zmienne pomocnicze:

• l - przechowuje indeks lewego krańca tablicy,

• p - przechowuje indeks prawego krańca tablicy,

• sr - przechowuje indeks środkowego elementu tablicy

Lista kroków:

K1:    l ← 0  
K2:    p ← 15  
K3:    sr ← (l+p)/2  
K4:    Dopóki l <= p  
             wykonuj kroki od K5 do K7
K5:    Jeśli tab[sr] = szukana  
           zwróć sr
K6:    Jeśli tab[sr] > szukana  
              to p ← sr - 1
      inaczej l ← sr + 1
K7:    sr ← (l+p)/2  
K8:    zwróć -1 

Wynik działania:

Podaj liczbe ktora chcesz znalezc: 29
Liczba 29 wystepuje w zbiorze w komorce o indeksie: 9