Sortowanie przez Scalanie - teoria

Sortowanie przez scalanie (Merge Sort)

Sortowanie przez scalanie to algorytm sortowania oparty na metodzie "dziel i rządź" (divide and conquer). Jego główna idea polega na podziale tablicy na mniejsze fragmenty, sortowaniu ich oddzielnie, a następnie łączeniu (scalaniu) w jedną posortowaną całość.

Zasada działania algorytmu

1. Podziel problem na mniejsze części

   • Jeśli tablica zawiera więcej niż jeden element, podziel ją na dwie (prawie równe) części.

   • Proces ten jest powtarzany rekursywnie, aż każda podtablica będzie miała tylko jeden element (a taka tablica jest już posortowana).

2. Posortuj każdą z części (rekurencyjnie)

   • Każda podtablica jest sortowana osobno za pomocą tego samego algorytmu.

3. Scal posortowane podtablice w jedną całość

   • Dwie posortowane tablice są łączone w jedną, porównując elementy z obu podtablic i układając je w odpowiedniej kolejności.

   • Proces ten jest powtarzany aż do momentu, gdy cała tablica będzie posortowana.

Przykład działania krok po kroku

Rozważmy tablicę:

[38, 27, 43, 3, 9, 82, 10]

Krok 1: Dzielimy tablicę na dwie części

[38, 27, 43, 3]    |    [9, 82, 10]

Dzielimy ponownie:

[38, 27] | [43, 3]     |     [9, 82] | [10]

Dzielimy dalej, aż każda część zawiera pojedynczy element:

[38] [27] | [43] [3]    |    [9] [82] | [10]

Krok 2: Scalanie posortowanych podtablic

Scalamy małe fragmenty w większe, zachowując porządek:

[27, 38] | [3, 43]    |    [9, 82] | [10]

Scalamy dalej:

[3, 27, 38, 43] | [9, 10, 82]

Ostateczne scalanie daje nam:

[3, 9, 10, 27, 38, 43, 82]  (tablica posortowana)

Przykład - wizualizacja

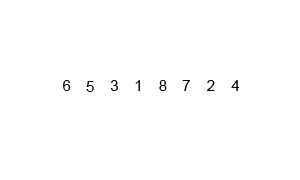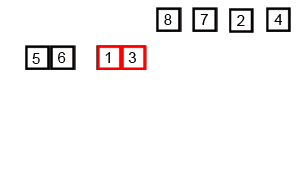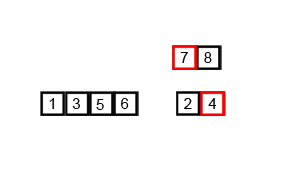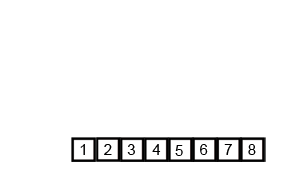
Źródło: Jakub Piskorowski

Przykład - wykres słupkowy

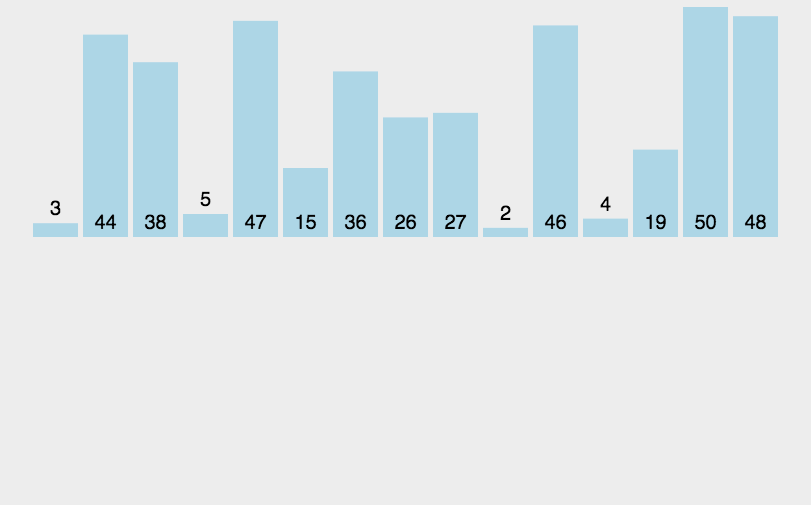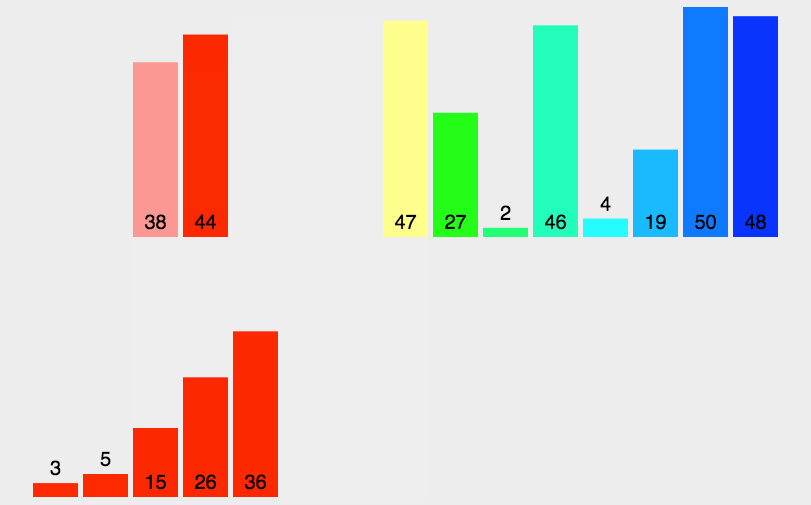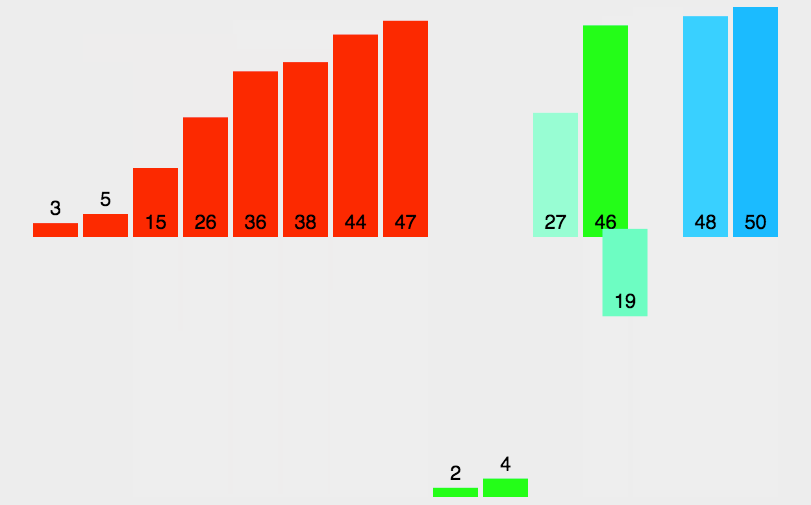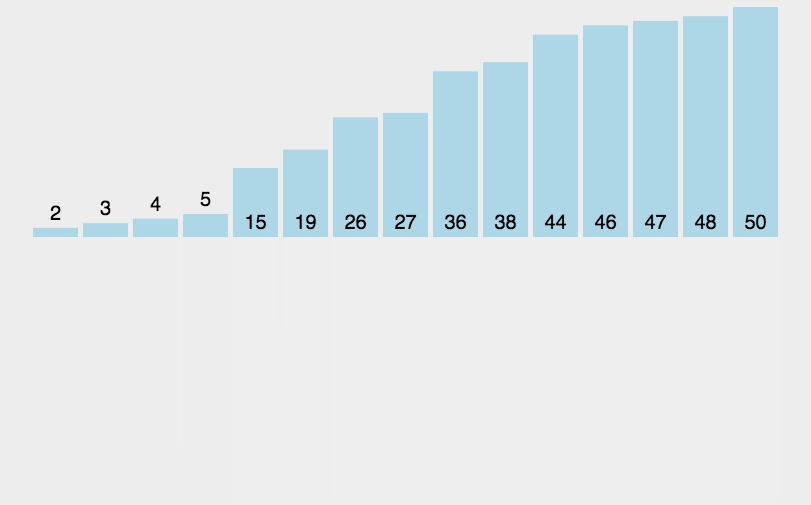
Źródło: Jakub Piskorowski

Pseudokod - sortowanie przez scalanie

W każdym kroku algorytmu sortowania przez scalanie tablica jest sukcesywnie dzielona na dwie mniejsze części, aż do osiągnięcia jednoelementowych podtablic. Następnie poszczególne fragmenty są stopniowo scalane w sposób uporządkowany poprzez porównywanie najmniejszych dostępnych wartości z obu podtablic. Dzięki temu unika się konieczności wielokrotnego przeszukiwania tablicy, co znacząco zwiększa efektywność sortowania.

W funkcji MergeSort poprzez wywołanie rekurencyjne dzielimy tablice na dwie części. Na prawą i lewą stronę.

void MergeSort(int* tab, int l, int r) {
    if (r > l) {
        int m = (l + r) / 2;
        MergeSort(tab, l, m);   // Podzielenie tablicy na lewa strone
        MergeSort(tab, m + 1, r);   // Podzielenie tablicy na prawa strone
        Merge(tab, l, m, r);
    }
}

Funkcja "Merge"

Należy napisać funkcję, która, po uprzednim podzieleniu tablicy na mniejsze części, wykona prostą operacje porównania oraz na nowu połączy tablice.

Wejście:

• tab - tablica z losowymi wartościami liczb całowitych

• l - indeks lewej strony tablicy

• m - indeks środka tablicy

• r - indeks prawej strony tablicy

Zmienne pomocnicze:

• lSize - przechowywanie rozmiaru lewej tablicy

• rSize - przechowywanie rozmiaru prawej tablicy

• indexL - przechowująca indes lewej tablicy podczas operacji łączenia tablic

• indexR - przechowująca indes prawej tablicy podczas operacji łączenia tablic

Tablice pomocnicze

• tabL - przechowująca tymczasowo wartości lewej tablicy

• tabR - przechowująca tymczasowo wartości prawej tablicy

Lista kroków:

K1:   lSize ← m - l + 1
K2:   rSize ← r - m
K3:   tabL[lSize]   Tablica pomocnicza
K4:   tabR[rSize]   Tablica pomocnicza

K5   Dla x = 0,1,...,lSize   Kopiowanie danych do tablic pomocniczych
        wykonuj tabL[] ← tab[l+x]
K6:   Dla y = 0,1,..., rSize   Kopiowanie danych do tablic pomocniczych
        wykonuj tabR[] ← tab[m+1-y]

K7:   indexL ← 0
K8:   indexR ← 0
K9:   currIndex = l

K10:   Dopóki indexL < lSize oraz indexR < rSize   Łaczenie tablicy prawej (R) oraz lewej (L)
        wykonuj kroki od K11 do K12
K11:   Jeżeli tabL[indexL] <= tabR[indexR]
        to tab[currIndex] ← tabL[indexL++]
        inaczej tab[currIndex] ← tabR[indexR++]
K12:   currIndex++

K13:   Dopóki indexL < lSize   Jeśli w tablicy(tabL) zostały jeszcze jaieś elementy to kopiujemy je
        to tab[currIndex++] = tabL[indexL++]
K14:   Dopóki indexR < rSize   Jeśli w tablicy(tabR) zostały jeszcze jaieś elementy to kopiujemy je
        to tab[currIndex++] = tabR[indexR++]

K15:   delete[] tabL
K16:   delete[] tabR

Wynik działania programu:

Wprowadz liczbe elementow do posortowania: 8

Tablica przed posortowaniem:
70 | 36 | 86 | 71 | 22 | 71 | 89 | 77 |

Rozpoczecie sortowania

Tablica po sortowaniu:
22 | 36 | 70 | 71 | 71 | 77 | 86 | 89 |