Metoda połowienia przedziałów - teoria

Omawiany algorytm wyznacza miejsce zerowe z dokładnością do pewnego ϵ (epsilon) (dokładność tą ustalamy na początku programu) w przedziale obustronnie domkniętym [a,b] przy następujących założeniach:

• Funkcja jest ciągła (oznacza to, że jej wykres narysujemy nie odrywając ołówka, chodź definicja funkcji ciągłej jest znacznie bardziej złożona)

• W przedziale [a,b] funkcja ma dokładnie jedno miejsce zerowe.

Przyjrzyjmy się poniższemu rysunkowi spełniającemu powyższe założenia:

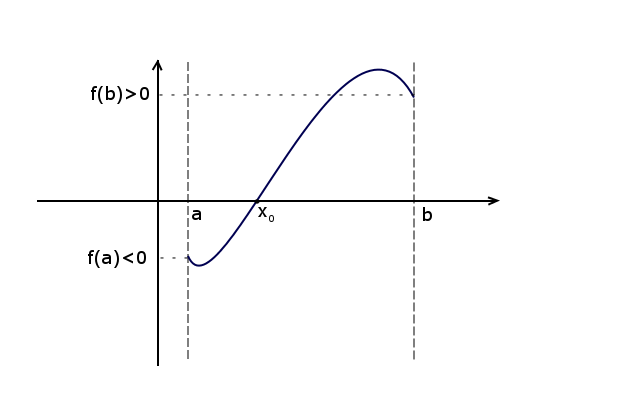
Źródło: Jakub Piskorowski

Dla każdej takiej funkcji będzie zachodził warunek:

• f(a) * f(b) < 0

ponieważ wartości na krańcach przedziałów będą zawsze przeciwnych znaków (chyba, że miejsce zerowe znajduje się w jednym z krańców).

W pierwszym kroku wyznaczamy środek przedziału i sprawdzamy, czy nie jest on już miejscem zerowym. Jeśli nie to sprawdzamy czy:

• f(a) * f(srodek) < 0

Jeśli tak, to miejsce zerowe musi znajdować się w przedziale:

• [a, srodek)

w przeciwnym razie w przedziale:

• (srodek, b]

W pierwszej sytuacji wartość b zostanie zastąpiona wartością środka, w drugiej wartość a.

W omawianym przykładzie zachodzi sytuacja pierwsza:

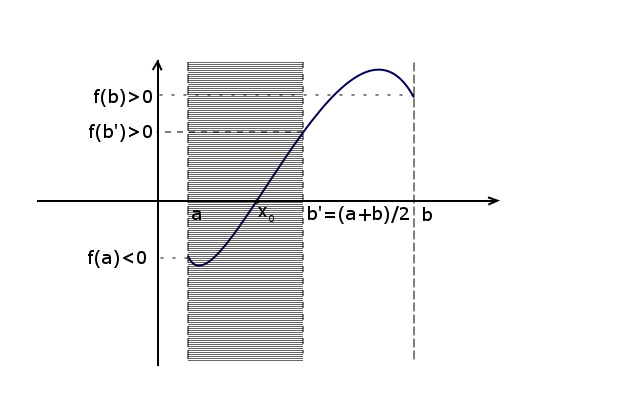
Źródło: Jakub Piskorowski

Czynności dzielenia przedziału [a, b] powtarzamy do momentu, aż nie będzie spełniony warunek ϵ < a−b.

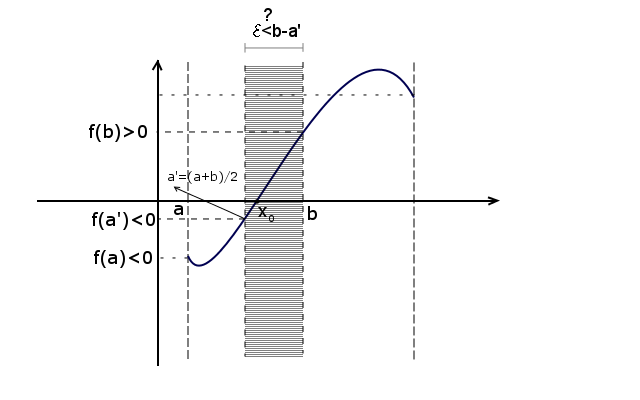
Źródło: Jakub Piskorowski

Gdy osiągniemy szukaną dokładność, tzn. b - a <= ϵ, możemy wypisać miejsce zerowe, które przyjmuje wartość (b-a) / 2.

Przedstawiony algorytm szuka miejsca zerowego dla wielomianu:

• f(x) = x³ - 3x² + 2x - 6

który spełnia podane na początku artykułu założenia. Program wyznacza miejsce zerowe z dokładnością do pięciu miejsc po przecinku.

Pseudokod - Metoda połowienia przedziałów (iteracyjnie)

Funkcja f

Rozpatrujemy wielomian f(x) = x³ - 3x² + 2x - 6
Rozbijamy go schematem Hornera i obliczamy jego wartość.

Wejście:

• x - argument funkcji

Lista kroków:

K1:   zwróć x*(x*(x-3)+2)-6;  

Funkcja połowienia przedziałów

Wejście:

• a = -10 – lewy kraniec przedziału

• b = 10 - prawy kraniec przedziału

• epsilon = 0.00001 - dokładność wyznaczania miejsca zerowego

Zmienne pomocnicze:

• srodek - wyznaczenie srodka, przedziału

Lista kroków:

K1:   jeżeli f(a) = 0.0
      zwróć a
K2:   jeżeli f(b) = 0.0
      zwróć b
K3:   dopóki b-a > epsilon
      wykonuj kroki K4...k6
K4:   srodek ← (a+b)/2
K5:   jeżeli f(srodek) = 0   jeżeli miejsce zerowe jest w środku
      zwróć środek
K6:   jeżeli f(a)*f(srodek) < 0
      b ← środek
      w przeciwnym razie a ← srodek
K7:   zwróć (a+b)/2

Wynik działania programu:

Znalezione miejsce zerowe wynosi: 3.00000

Pseudokod - Metoda połowienia przedziałów (rekurencyjnie)

Funkcja f

Rozpatrujemy wielomian f(x) = x³ - 3x² + 2x - 6
Rozbijamy go schematem Hornera i obliczamy jego wartość.

Wejście:

• x - argument funkcji

Lista kroków:

K1:   zwróć x*(x*(x-3)+2)-6;  

Funkcja połowienia przedziałów

Wejście:

• a = -10 – lewy kraniec przedziału

• b = 10 - prawy kraniec przedziału

• epsilon = 0.00001 - dokładność wyznaczania miejsca zerowego

Zmienne pomocnicze:

• srodek - wyznaczenie srodka, przedziału

Lista kroków:

K1:  jeżeli f(a) = 0.0
      zwróć a
K2:   jeżeli f(b) = 0.0
      zwróć b
K3:   srodek ← (a+b)/2
K4:   jeżeli b-a <= epsilon
      zwróć środek
K5:   jeżeli f(a)*f(srodek) < 0
      zwroc PolowieniePrzedzialow(a, srodek, epsilon)
K6:   zwróć PolowieniePrzedzialow(srodek, b, epsilon)

Wynik działania programu:

Znalezione miejsce zerowe wynosi: 3.00000