Dziesiętna na binarną - teoria

Zamiana liczby dziesiętnej na binarną

Zamiana liczby dziesiętnej na binarną polega na znalezieniu odpowiednich potęg liczby 2, które sumują się do liczby wejściowej.

Każda pozycja w liczbie binarnej odpowiada kolejnej potędze dwójki:

• Najmłodsza cyfra (z prawej strony) to 2⁰,

• Kolejna to 2¹,

• Następnie 2²,

• I tak dalej.

Jak to zrobić?

1. Dziel liczbę dziesiętną przez 2 i zapisuj reszty:

   • Reszta z dzielenia przez 2 to kolejna cyfra binarna, liczona od prawej strony.

   • Kontynuuj dzielenie wyniku całkowitego przez 2, aż do uzyskania 0.

2. Odczytaj wynik binarny od dołu do góry:

   • Pierwsza reszta to najmłodsza cyfra (LSB – least significant bit),

   • Ostatnia reszta to najstarsza cyfra (MSB – most significant bit).

Przykład: Zamiana liczby 26 na system binarny

Zamiana liczby dziesiętnej 26 na system binarny krok po kroku z użyciem dzielenia przez 2:

• 26÷2=13 (reszta 0)

• 13÷2=6 (reszta 1)

• 6÷2=3 (reszta 0)

• 3÷2=1 (reszta 1)

• 1÷2=0 (reszta 1)

Czytając reszty od dołu, mamy: 11010.

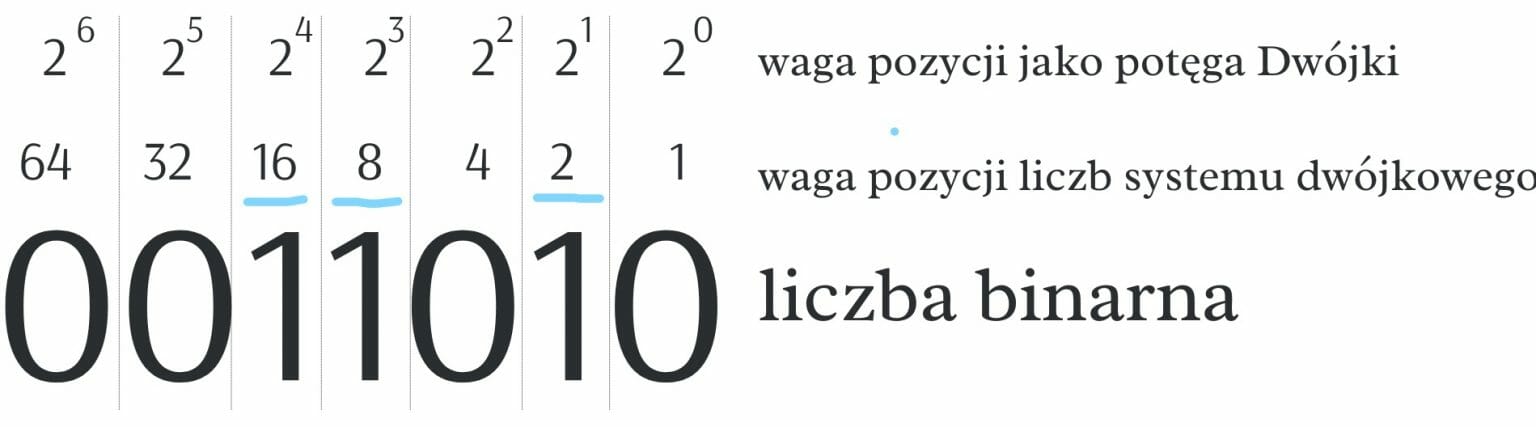
Źródło: Jakub Piskorowski

Pseudokod - konwersji liczby dziesiętnej na binarną

Funkcja algorytmu konwersji liczby dziesiętnej na binarną:

Wejście:

• liczba - liczba dziesietna

Lista kroków:

K1:   tab[15]   deklaracja tablicy o rozmiarze 31
K2:   i ← 0   deklaracja iteratora
K3:   dopóki liczba jest różna od zera
      wykonuj kroki k4...k5
K4:   tab[i++] ← liczba modulo 2   zapisujemy resztę z dzielenia w kolejnym elemencie tablicy
K5:   liczba ← liczba / 2
K6:   od j ← i-1 do j >=0
      wykonuj krok k7
K7:   wyświetl element tablicy z indeksem j

Wynik działania programu:

Podaj liczbe dziesietna: 26
Liczba 26 po zamianie na postac binarna: 11010